系统 ID 模式操作¶
系统识别模式(SYSID 模式)提供了一种利用飞行测试数据开发高精度飞行动力学模型(也称为数字孪生模型)的快速方法。这些由实际飞行器数据生成的模型可用于数学模型验证和改进(如果已有模型),也可完全取代现有模型。还可以对控制法则进行调整,包括模拟闭环飞行器的响应。
作为适航认证的一部分,这些模型和相关的控制律分析在证明所需的稳定性指标方面非常有价值。
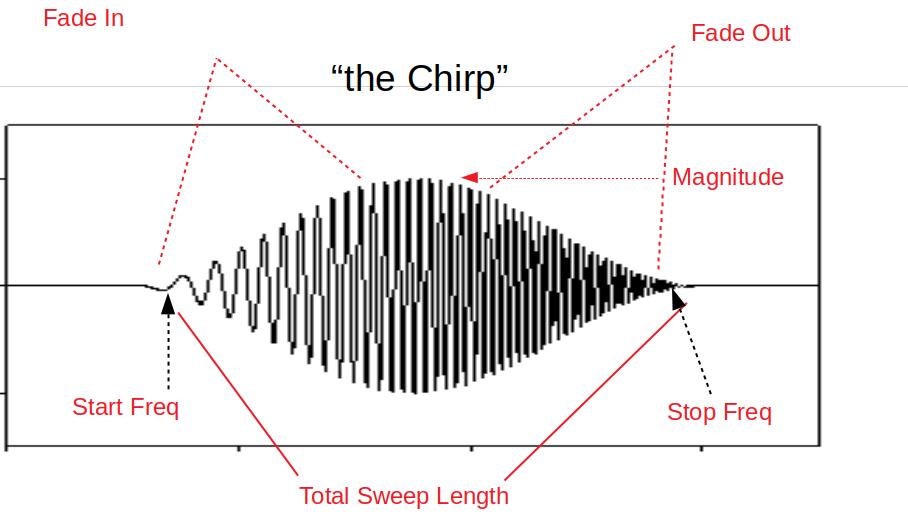
这种飞行模式会产生一组数据,包括刺激(激励)信号和测量到的反应,这些数据都记录在数据闪存日志中。根据创建模型的目的,这些信号在(飞行)控制器的特定部位注入和收集。注入信号("啁啾")通过(飞行)控制器控制结构传播,直至输出到物理执行器,使载具对注入信号做出反应。啁啾 "的频率扫描和振幅可通过参数以及注入点进行设置。
然后,(飞行)控制器的内部传感器会对飞行器的电气/机械反应进行监测并记录。通过记录这些传感器的输出并将其与刺激(注入的 "啁啾 "信号)进行比较,工程师可以深入了解飞机的电气/机械特性和相互作用。
数据收集¶
数据收集通过切换到系统 ID 模式启动。每次切换到系统 ID 飞行模式,都会启动新的数据采集。要改变激励振幅,可使用 SID_MAGNITUDE 参数可以使用 第 6 声道飞行稳定调整旋钮 在数据收集期间。
系统 ID 模式提供了这些功能:
确保采取有效的安全措施,防止飞机因注入信号而进入不安全的飞行状态
提供一种机制来选择激发信号的注入位置
启动系统识别程序
实施基于啁啾的刺激信号,其中包括
振幅
启动频率
停止频率
记录时间
淡入时间
淡出时间
使用飞行稳定调整旋钮调节刺激振幅
记录生成的数据,包括
混音器输入数据
IMU 输出数据
调整子采样率
记录¶
系统识别数据记录提供所需的参考和 IMU 数据。每个时间循环中的所有系统识别数据都在同一时间记录并放入数据闪存日志中,以确保数据的时间同步。SID 日志信息中新增了系统 ID 陀螺仪和加速度测量日志。这些信息是自上一循环时间以来的陀螺仪和加速度平均测量值,直接从 IMU 获取,无需任何额外过滤。这些数据来自 EKF 的三角角和三角速度。为该日志选择的 IMU 与用于在角度控制环路中生成姿态预测的 IMU 相同。
参数¶
SID_AXIS:控制激发哪个轴和控制回路注入点
值:0:无(阻止进入模式和显示其他模式参数),1:输入滚动角,2:输入俯仰角,3:输入偏航角,4:恢复滚动角,5:恢复俯仰角,6:恢复偏航角,7:速率滚动,8:速率俯仰,9:速率偏航,10:混合器滚动,11:混合器俯仰,12:混合器偏航,13:混合器推力
SID_MAGNITUDE:系统识别啁啾幅度。根据注入点的不同,单位为 deg、deg/s 或混频器输出的 0-1。可以使用 飞行稳定调整旋钮 使用 58 选项。
SID_F_START_HZ:系统识别 启动频率。范围: 0.01-100 Hz0.01-100 赫兹
SID_F_STOP_HZ:扫频结束时的频率。范围: 0.01-100 Hz0.01-100 赫兹
SID_T_FADE_IN:达到扫描最大振幅的时间。范围: 0-20 秒0-20 s
SID_T_REC:系统识别总扫描长度。范围: 0-255 秒0-255 s
SID_T_FADE_OUT:扫描结束时振幅归零的时间。范围: 0 至 5 秒0 至 5 秒
记录速率由 ATTITUDE_FAST 和 ATTITUDE_MEDIUM 位设置。 LOG_BITMASK.记录速率是主回路频率除以子采样系数。
ATTITUDE_FAST |
ATTITUDE_MED |
速率分配器 |
1 |
1 |
1 |
1 |
0 |
2 |
0 |
1 |
4 |
0 |
0 |
8 |
下图描述了 SID_AXIS 黄色的注入点和最内层 PID 循环的一些细节,当 汇率 == 0.
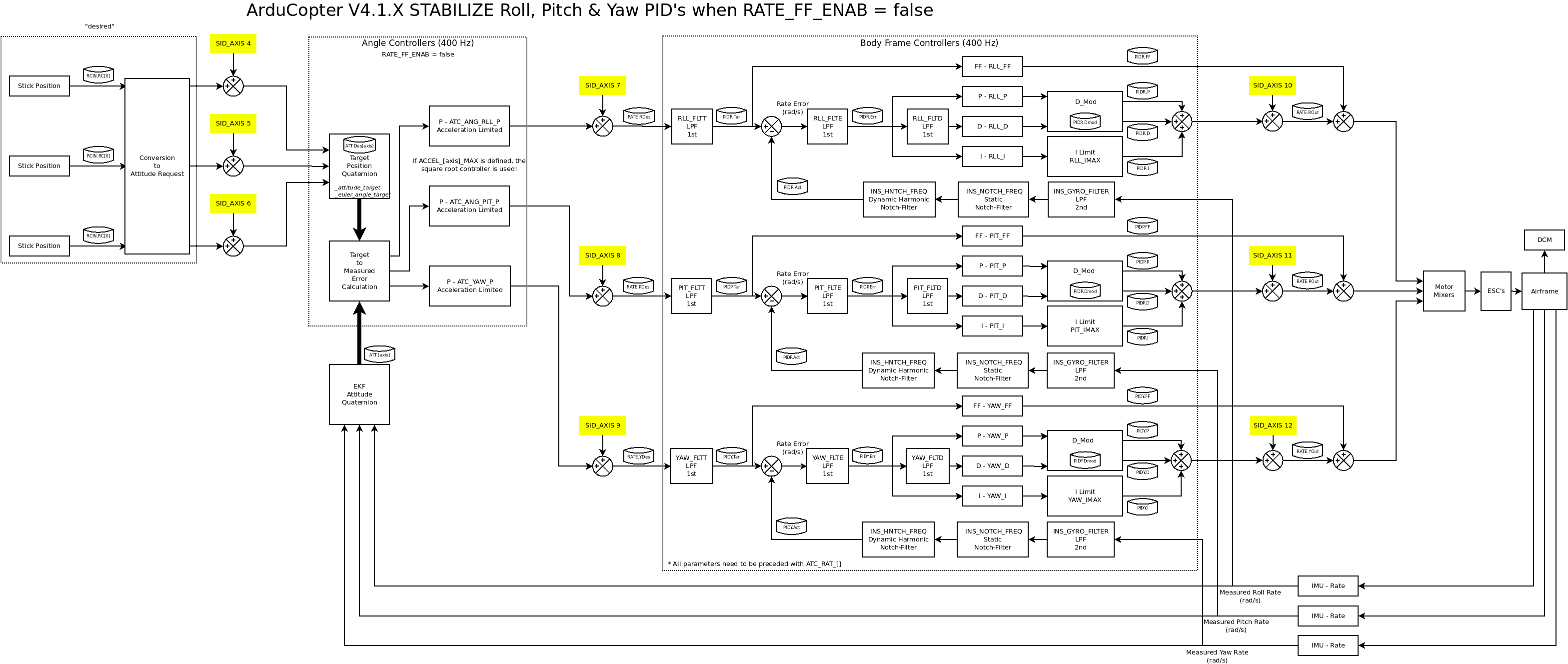
ATC_RATE_FF_ENAB=0 时的 ArduCopter 控制回路
下图描述了 SID_AXIS 黄色的注入点和最内层 PID 循环的一些细节,当 汇率 == 1.
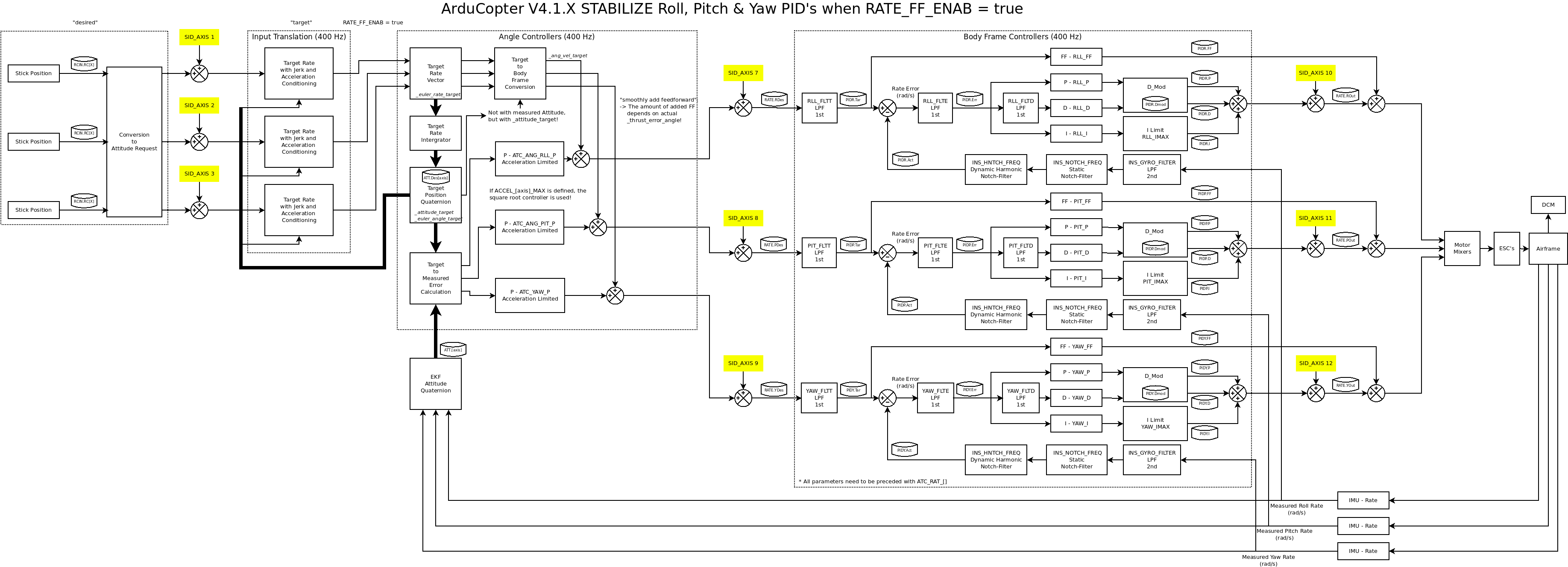
ATC_RATE_FF_ENAB=1 时的 ArduCopter 控制回路
识别多旋翼飞行器¶
型号范围¶
下面的框图描述了完整的飞行器控制系统及其组件。系统识别将为电机混合器、电机和电子速度控制器(ESC)以及旋翼飞行器机身创建一个数学模型。这种数学模型在控制文献中被称为工厂模型。频率扫描输入 SID_AXIS [10、11、12] 用于识别,因为它们通过叠加混频器输入,向被视为系统提供直接输入 \(\delta_{rll}\), \(\delta_{pit}\) 和 \(\delta_{yaw}\) 与刺激信号一起输入。与其他啁啾输入信号相比,控制器对这些输入信号的修改较少。工厂的输入控制信号必须是持续激励的,这意味着啁啾信号不会被控制器抵消。必须相应地选择啁啾信号的幅度。这样才能确保工厂模型输入端的波形大多为啁啾波。默认控制器参数较低,因此速率控制器输出的幅度也相对较低。
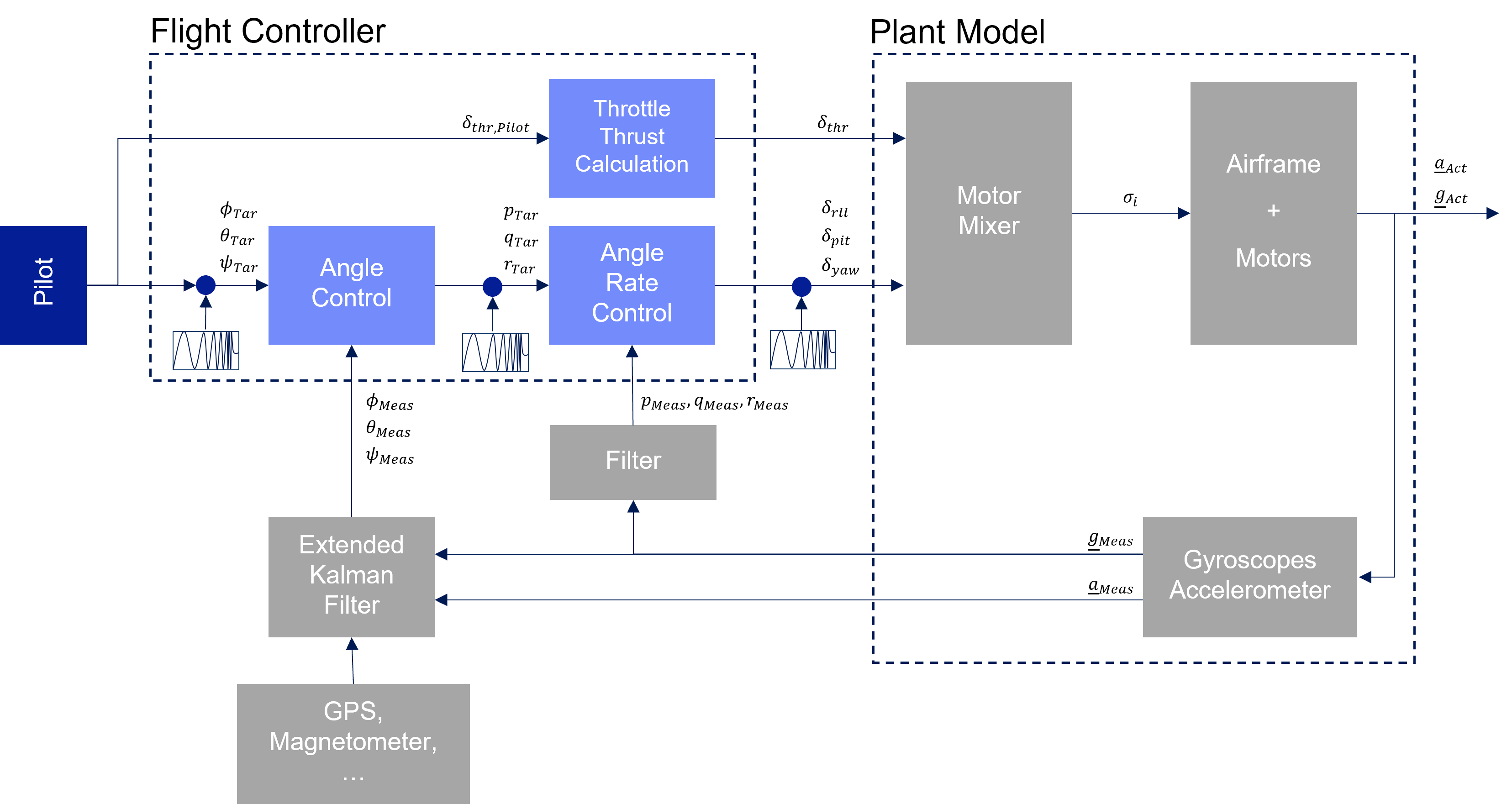
ArduPilot 控制系统
模型结构¶
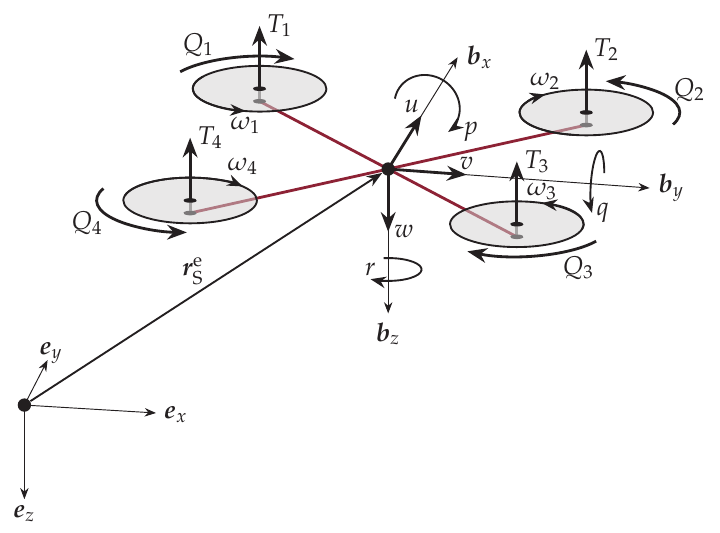
四车身示意图
四旋翼飞行器模型基于其运动方程。将四旋翼飞行器视为一个刚体,它有 6 个自由度,包括三个平移运动和三个旋转运动。上图显示的是四旋翼飞行器在由矢量 (\(e_{x}\), \(e_{y}\), \(e_{z}\)).四旋翼飞行器有自己的重心坐标系,称为机身固定坐标系。其坐标轴由矢量 (\(b_{x}\), \(b_{y}\), \(b_{z}\)). [1] 车身固定框架内的运动方程可表示为
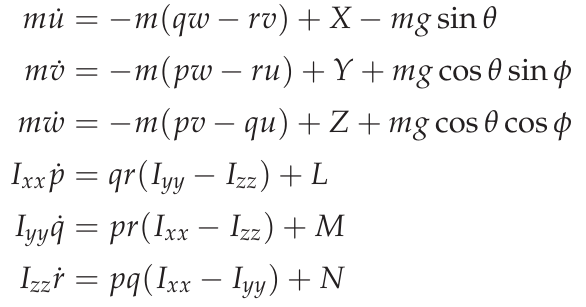
运动方程
其中 \(u\), \(v\) 和 \(w\) 是 \(b_{x}\), \(b_{y}\), \(b_{z}\) 方向,而 \(p\), \(q\), \(r\) 表示绕 \(x\), \(y\) 和 \(z\) 车身框架的轴线。变量 \(X\), \(Y\), \(Z\) 和 \(L\), \(M\), \(N\) 代表推力作用在机身上的力和扭矩 \(T_i\) 和反作用扭矩 \(Q_i\) 以及空气阻力和风造成的外力和力矩。 [2] \(\phi\) 和 \(\theta\) 是欧拉角,描述了飞行器在地球框架内的方位。推力和反作用力矩可用以下公式计算
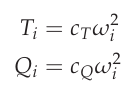
推力反扭矩方程
与 \(\omega_i\) 是螺旋桨的角速度,而 \(C_T\) 以及 \(C_Q\) 表示取决于螺旋桨几何形状的常数。根据这两个量,在 X 配置下,推进系统作用在旋翼飞行器机身上产生的力和扭矩可写成
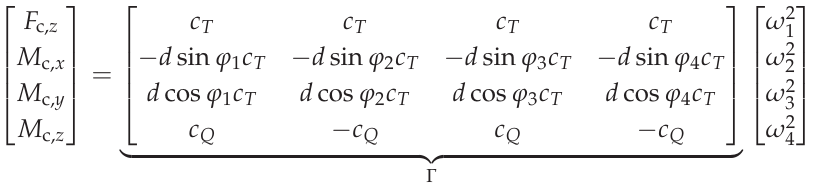
力矩分配矩阵
其中 \(d\) 代表各螺旋桨与机身重心之间的臂长,而 \(\varphi_i\) 代表螺旋桨臂相对于 \(b_x\) 旋翼飞行器的轴线。 [3] \(\Gamma\) 称为分配矩阵。
这些方程是非线性的,相互依存,难以使用。大多数控制系统分析和工具都基于较简单的线性或线性化系统。因此,通过观察状态变量和输入的微小干扰,围绕静止悬停状态对运动方程进行线性化。假设参数 MOT_THST_EXPO 一直以来 正确设置.
例如,横向速度 \(u\) 然后可以用它的静止条件来表示 \(u_0\) 及其扰动 \Delta u\)
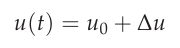
小扰动方程
悬停时,由于载具没有平移或旋转运动,因此每个状态和输入量的静止条件都是 0。 [4] 运动方程可简化为
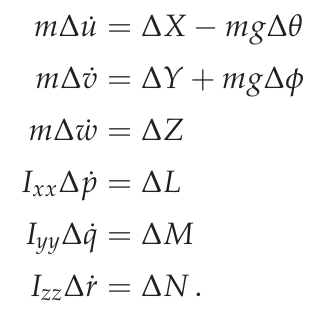
线性化运动方程
这种线性化消除了旋翼飞行器俯仰、翻滚和偏航运动之间的相互依存关系,从而产生了三个解耦系统。接下来,对每个力和扭矩的扰动进行建模,以获得这些系统输入对状态变量的影响。通过泰勒级数展开,力和力矩被描述为其所依赖的状态和输入变量扰动的线性函数。每个状态变量的系数都是各自力和转矩的所谓稳定或控制导数。 [4] [5]
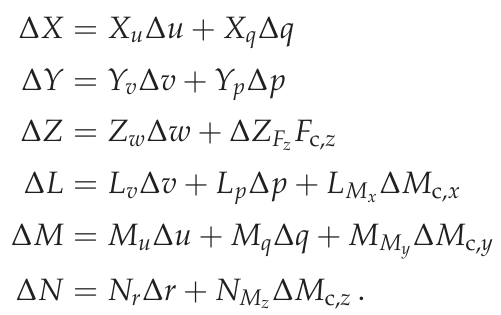
扰动力矩方程
通过插入这些力和力矩的描述,线性化运动方程被改写为状态空间表示法,控制力为 \(F_{c}\) 和扭矩 \(M_{c}\) 螺旋桨产生的扰动是模型的输入。由于方程中只包含扰动量,因此 \(\Delta\) 表示小扰动的数据被忽略。

如图所示,系统的实际控制输入是速率控制器的输出。 控制系统图.电机混合器将控制器输出转换为每个电机的推力需求。电机模型描述了从混合器输出到作用在机身上的控制力和扭矩的传递函数。电机无法立即实现混合器的要求。相反,它们有自己的动态需要建模。为此,假定推力需求与电调向电机提供的电压成正比关系。从电机电压到电机角速度的传递由一阶系统建模。 [2] 除此以外,还需要模拟电压与电机扭矩之间的关系,电机扭矩等于推进装置的反作用力矩 \(Q_i\).计算公式为 \(Q_i\) 在 推力反扭矩方程 仅模拟螺旋桨的静态反作用力矩。由于电机的惯性,电机的加速或减速会导致额外的动态反作用力矩。 [3] 因此,传递函数可写成
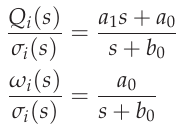
电机模型传递函数
电机的推力需求是根据控制器的输出计算得出的。 分配矩阵 [9]
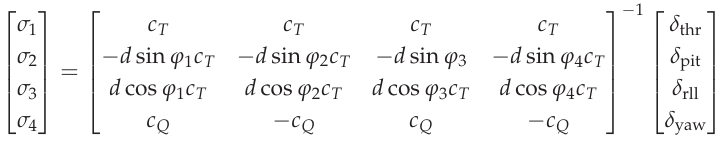
推力指令的控制输出
因此,上述倒转矩阵和 分配矩阵 相互抵消,从而留下以下四个独立的控制路径:摆动、滚动、俯仰和偏航。通过使用 传递函数 即控制器输出与作用在相应轴上的力或力矩之间的关系。为了在状态空间表示法中建立模型,需要将控制力和转矩添加到系统状态中。 [6] 滚轴、俯仰轴和偏航轴的状态空间模型分别为
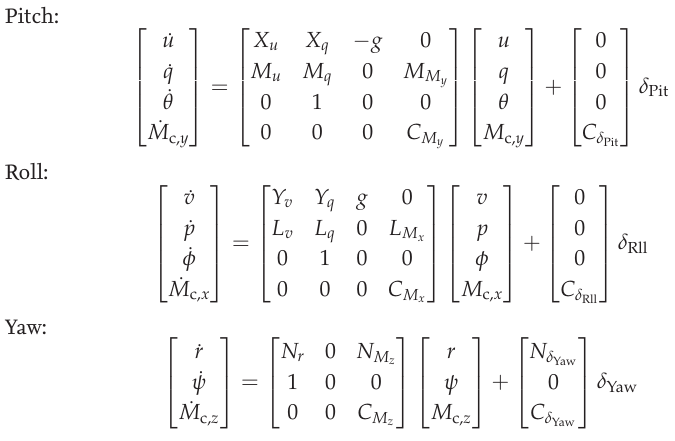
轴模型
通过拉普拉斯变换和角速度求解,可从上述状态空间模型得出各轴的传递函数模型。 \(p\), \(q\) 和 \(r\) 作为每个模型的输出。为简单起见,使用了通用系数。此外,还加入了死区时间项,以考虑建模时未考虑的延迟。 [6] 这三个传递函数代表了用于识别俯仰、滚动和偏航轴的模型结构。
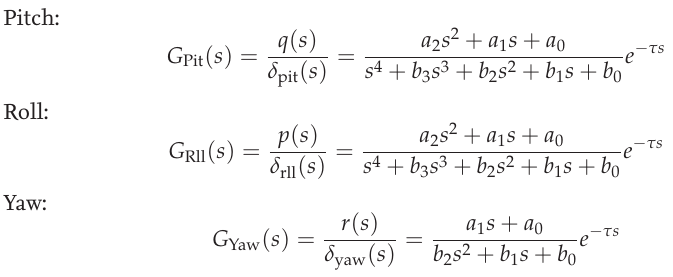
轴模型传递函数方程
识别过程示例¶
为了收集识别数据,需要对俯仰、滚动和偏航轴进行单独的 sysid 测试飞行。这一过程与飞行器的 PID 调整基本无关,可以在未调整的飞行器上进行。但调整必须足够稳定,以便飞行器安全飞行。因此 飞行稳定调整过程说明 但自动调整步骤可以跳过。在本节介绍的示例中,角度和速率控制器使用了默认参数。为防止速率控制器补偿过多的频率扫描信号,必须将每个轴的积分器增益设为零,并禁用角度控制器的前馈:
参数 |
价值 |
0 |
|
0 |
|
0 |
|
0 |
请确保载具在执行这些更改后保持稳定,如果不稳定,请有选择性地恢复这些更改。
本节将介绍一架相对较小的四旋翼飞行器的测试结果。它重 1.5 千克,臂长 22 厘米,配备 9 英寸螺旋桨。下表列出了每个轴的系统识别模式设置:
参数 |
价值 |
||
卷轴 |
间距 |
亚乌 |
|
10 |
11 |
12 |
|
0.15 |
0.15 |
0.55 |
|
0.05 赫兹 |
0.05 赫兹 |
0.05 赫兹 |
|
5 赫兹 |
5 赫兹 |
5 赫兹 |
|
5 s |
5 s |
5 s |
|
5 s |
5 s |
5 s |
|
130 s |
130 s |
130 s |
|
请根据自己载具的动力情况更改这些数值。频率范围的选择基于文献 [6] [10] 和飞行测试。如果使用较重和/或较大的系统,可能需要使用较低的频率来激发所需的动力。如果使用较轻和/或较小的系统,则可能需要使用较高的频率。
数据闪存日志用于获取飞行数据。速率控制器输出信号 RATE.ROut, RATE.POut 和 RATE.YOUT 使用。信号 SIDD.Gx, SIDD.Gy 和 SIDD.Gz 与测量到的旋翼飞行器角速率相对应。
下图显示了注入的频率扫描和由此产生的设备控制输入,即扫描和速率控制器输出的总和。滚动轴和俯仰轴的曲线图显示,系统激励减弱,尤其是在中频范围内。扫频衰减的原因是由于系统响应的幅度较大,控制器的输出被放大了(见下图 滚动响应 和 音高响应).虽然衰减了,但系统激励仍然足够大,可以获得可靠的频率响应和足够高的相干性,如下图所示。
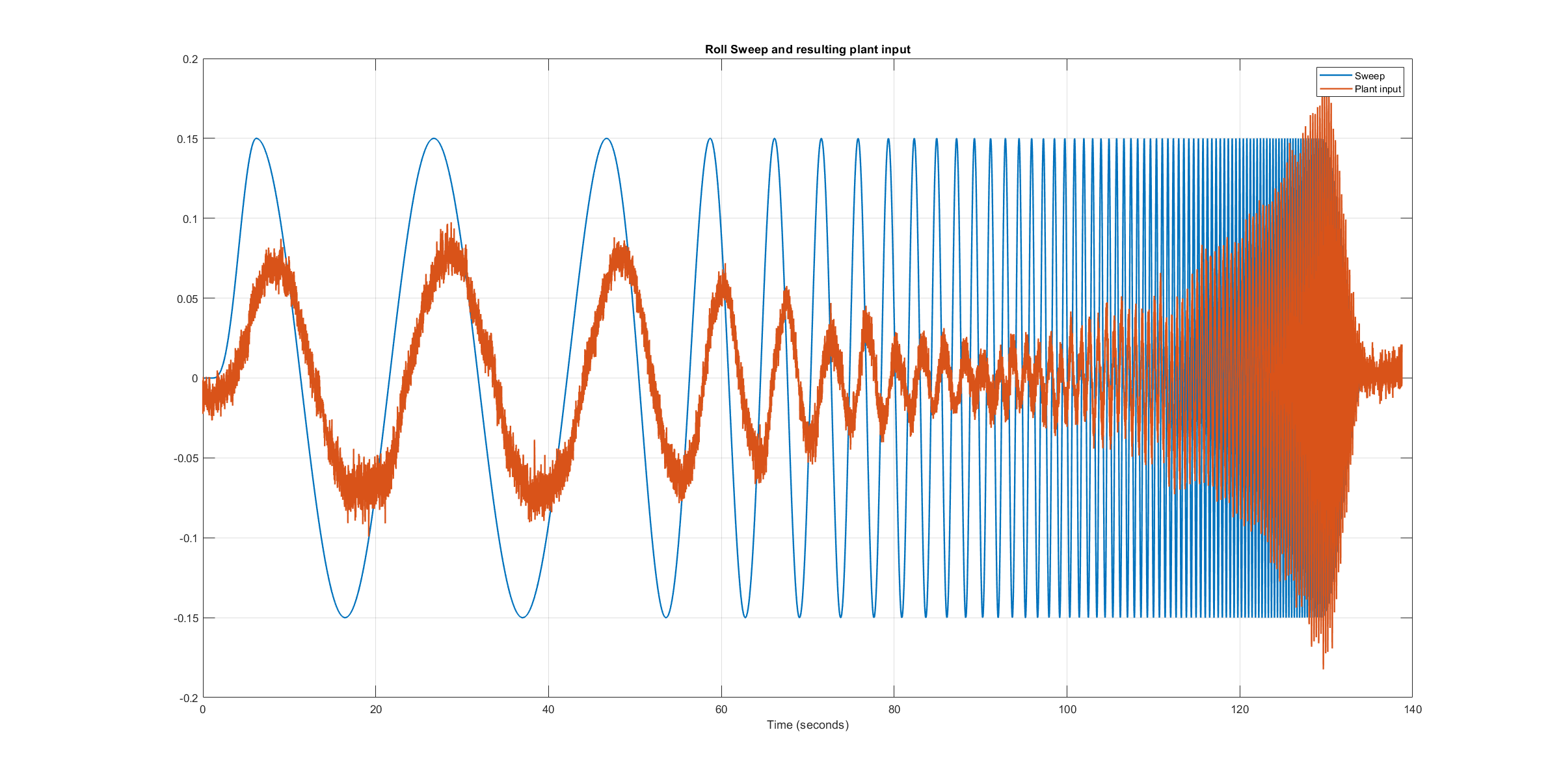
滚扫设备投入
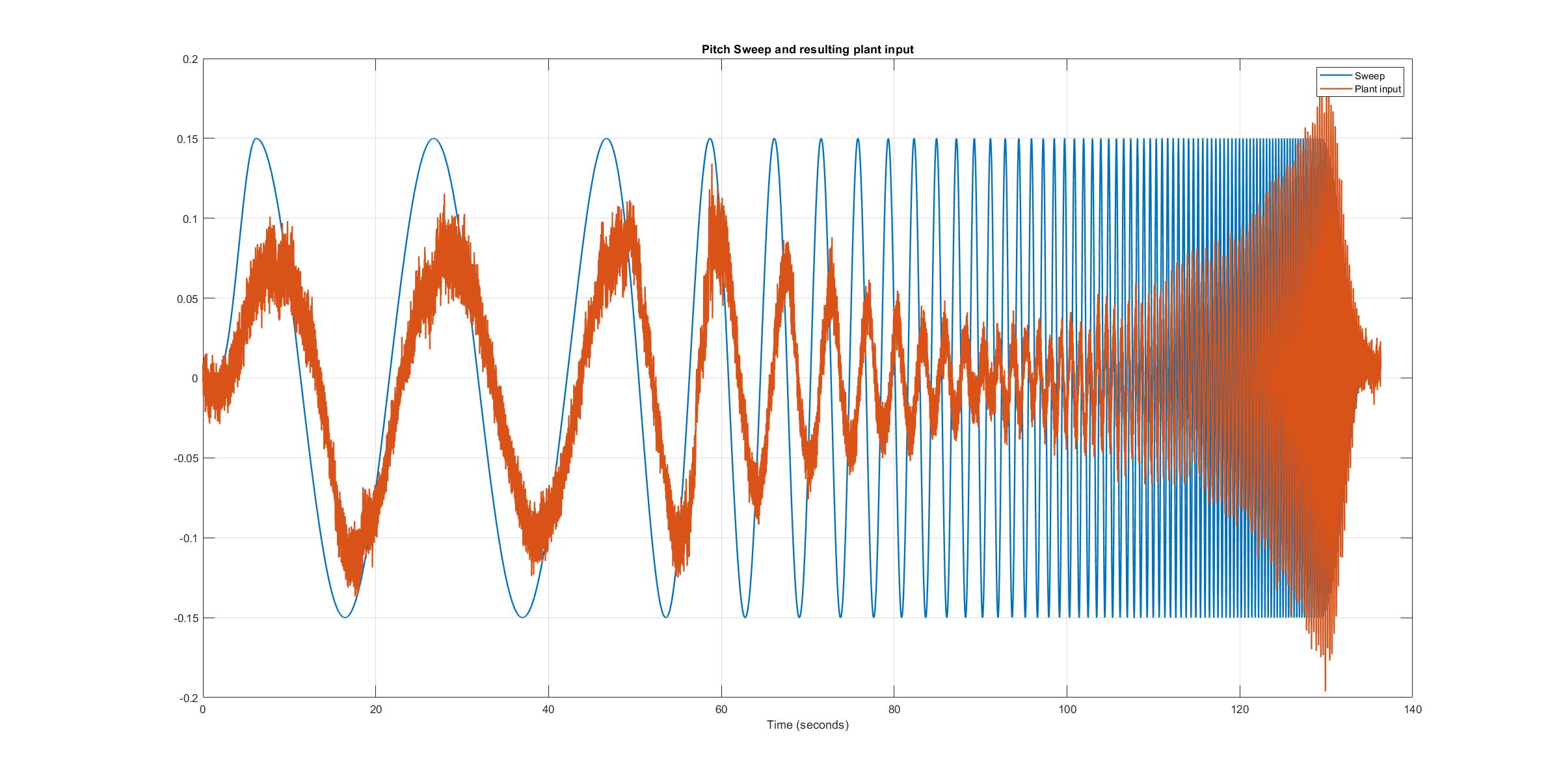
螺距扫描设备输入
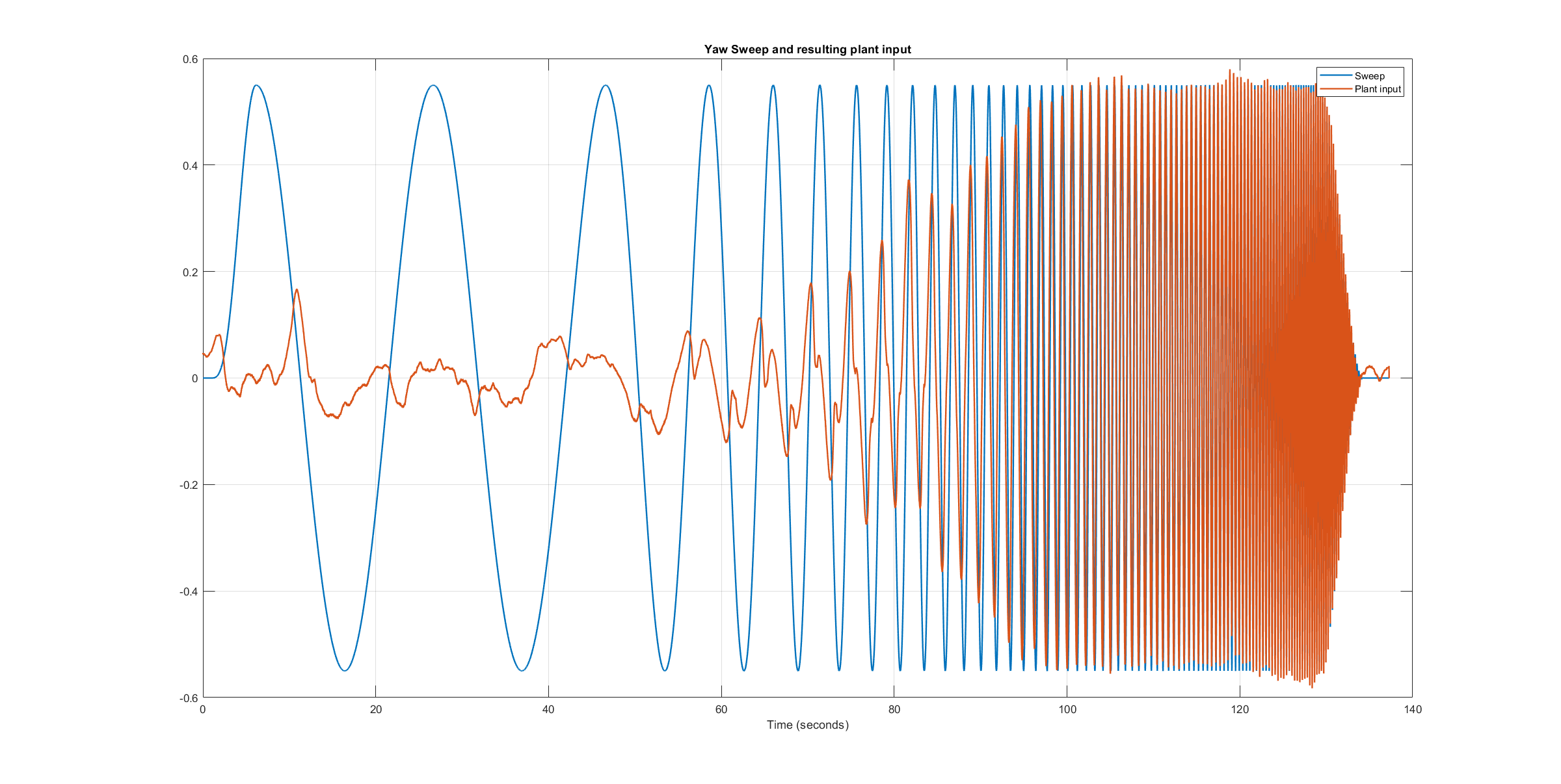
偏航扫频装置输入
通过对飞行数据进行频谱分析,可获得每个轴的频率响应。只有输入和输出之间具有足够一致性的测试飞行才会被用于系统识别。为了提高生成的设备模型的准确性并补偿过程误差,每个轴都要进行多次飞行,并计算出平均频率响应。下图显示了所有三个轴基于数据的频率响应。下图显示了输入和输出之间的一致性,它量化了输入和输出之间的线性关系。
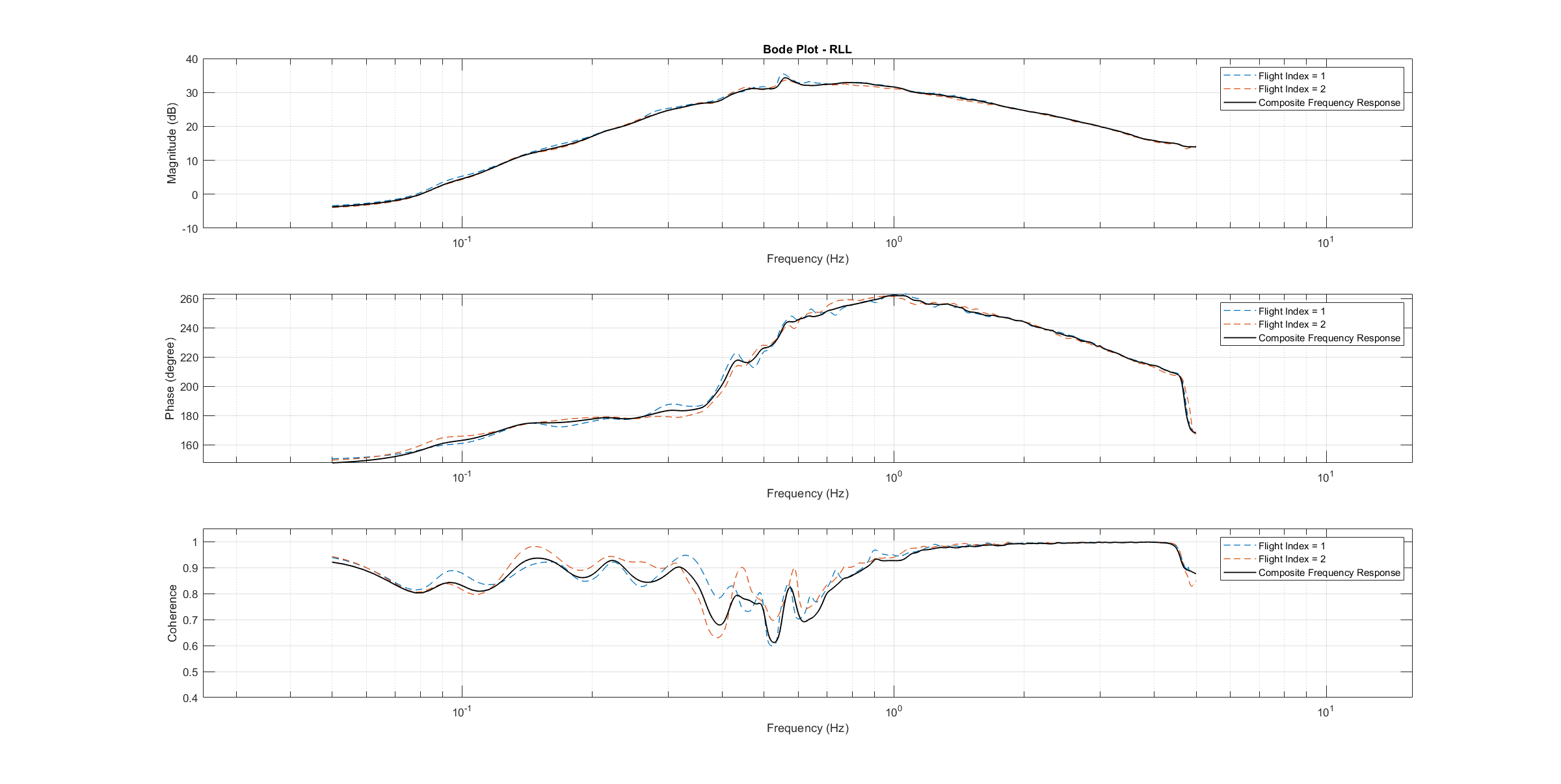
滚动博德图
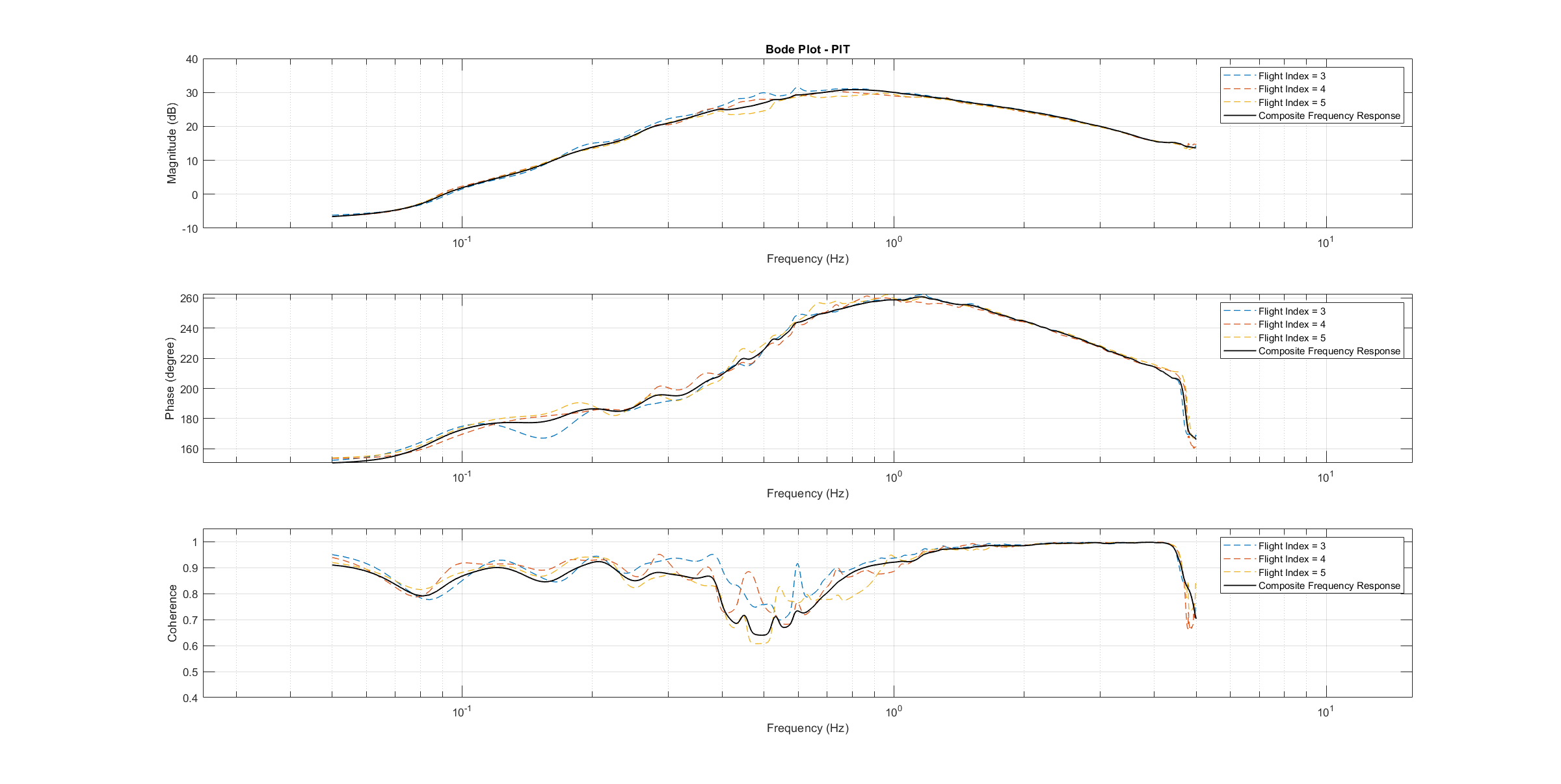
螺距 Bode 图
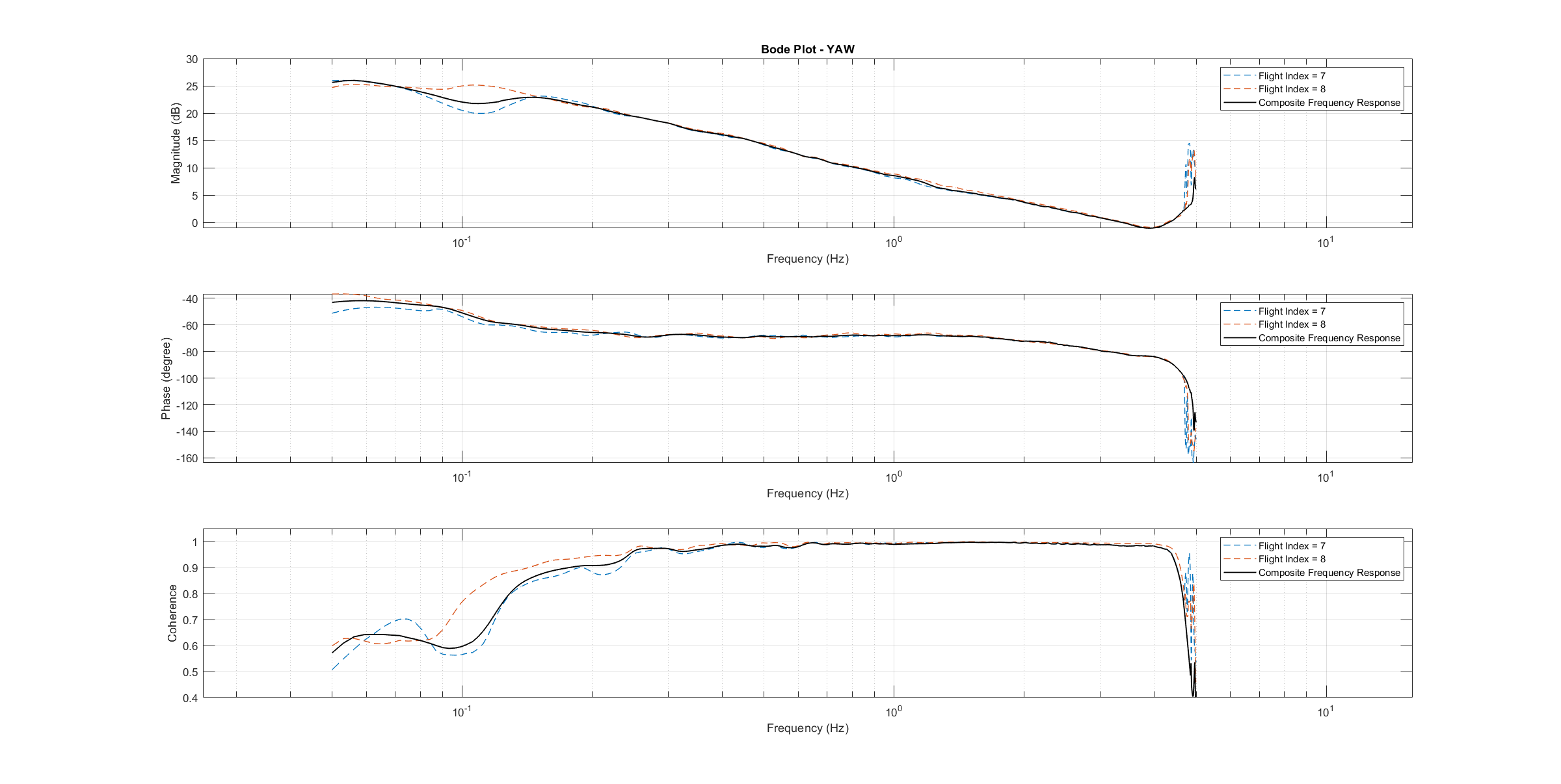
Yaw Bode 图
综合频率响应用于确定 传递函数模型.对设备模型传递函数的参数进行了优化,以最大限度地拟合收集到的实际数据频率响应。结果如以下三图所示。
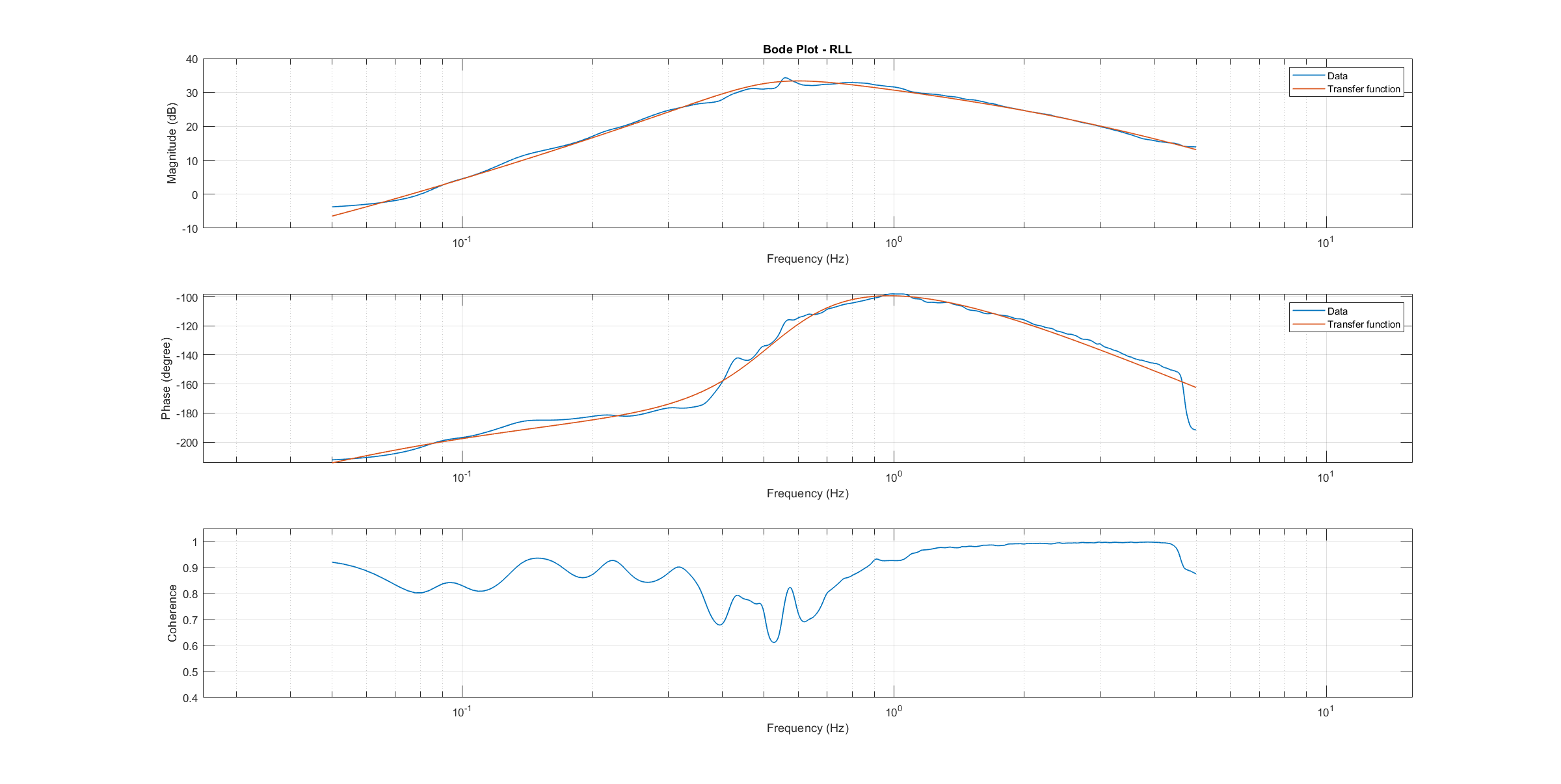
滚动传递函数
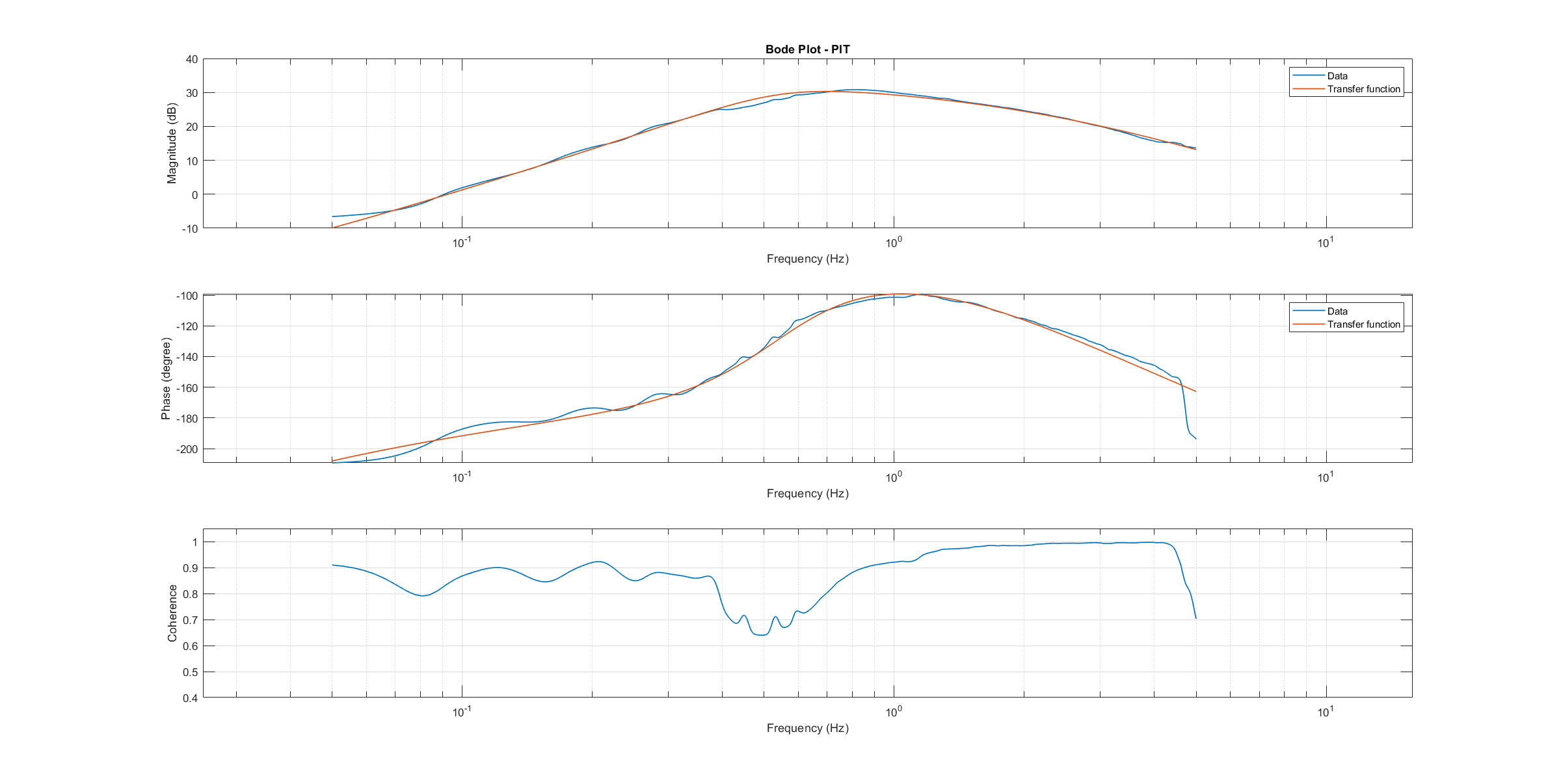
螺距传递函数
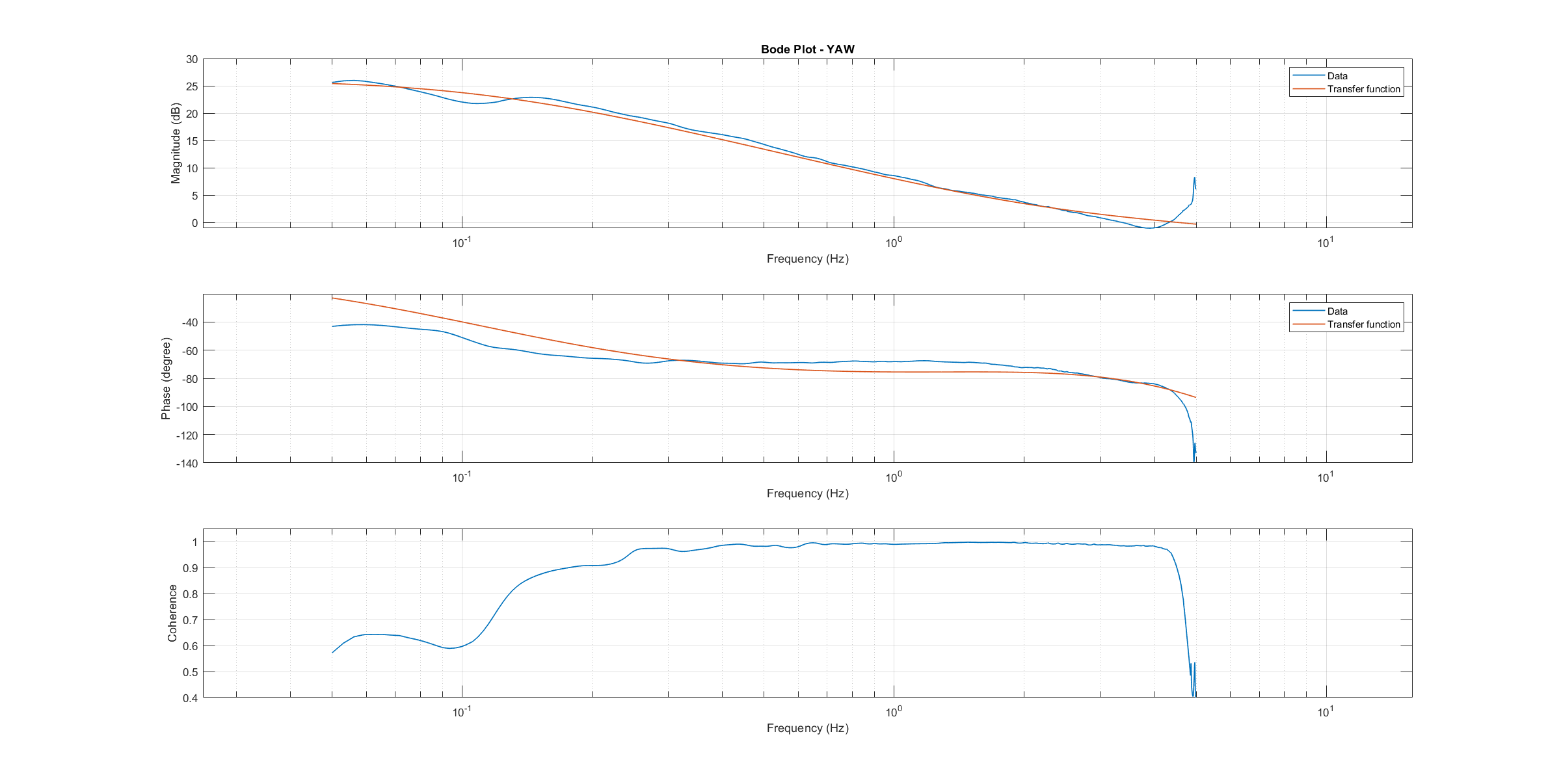
偏航传递函数
得出的传递函数模型如下

轴模型传递函数
识别结果和模型验证示例¶
四旋翼飞行器的系统本质上是不稳定的。轻微的建模错误或未考虑实际系统的外部输入,都会导致轴模型出现偏差 [7].由于模型无法完全再现真实系统的行为,因此模型验证在闭环中进行,并使用与试飞期间相同的稳定控制器。在验证测试运行中,闭环模型的输入信号与实际系统的输入信号相同,即稳定控制器的参考信号(所需角度或偏航轴的速率)。然后将模型的输出(即角速率)与实际飞行中测量的系统输出进行比较。首先,检查模型是否再现了测试信号,即频率扫描。稳定控制器的预期角度设为零,扫频直接加到速率控制器的输出中。
本章将介绍一架相对较小的四旋翼飞行器的测试结果。它重 1.5 千克,臂长 22 厘米,配备 9 英寸螺旋桨。从下面三张图中可以看出,每个模型都能再现测得的角速率。
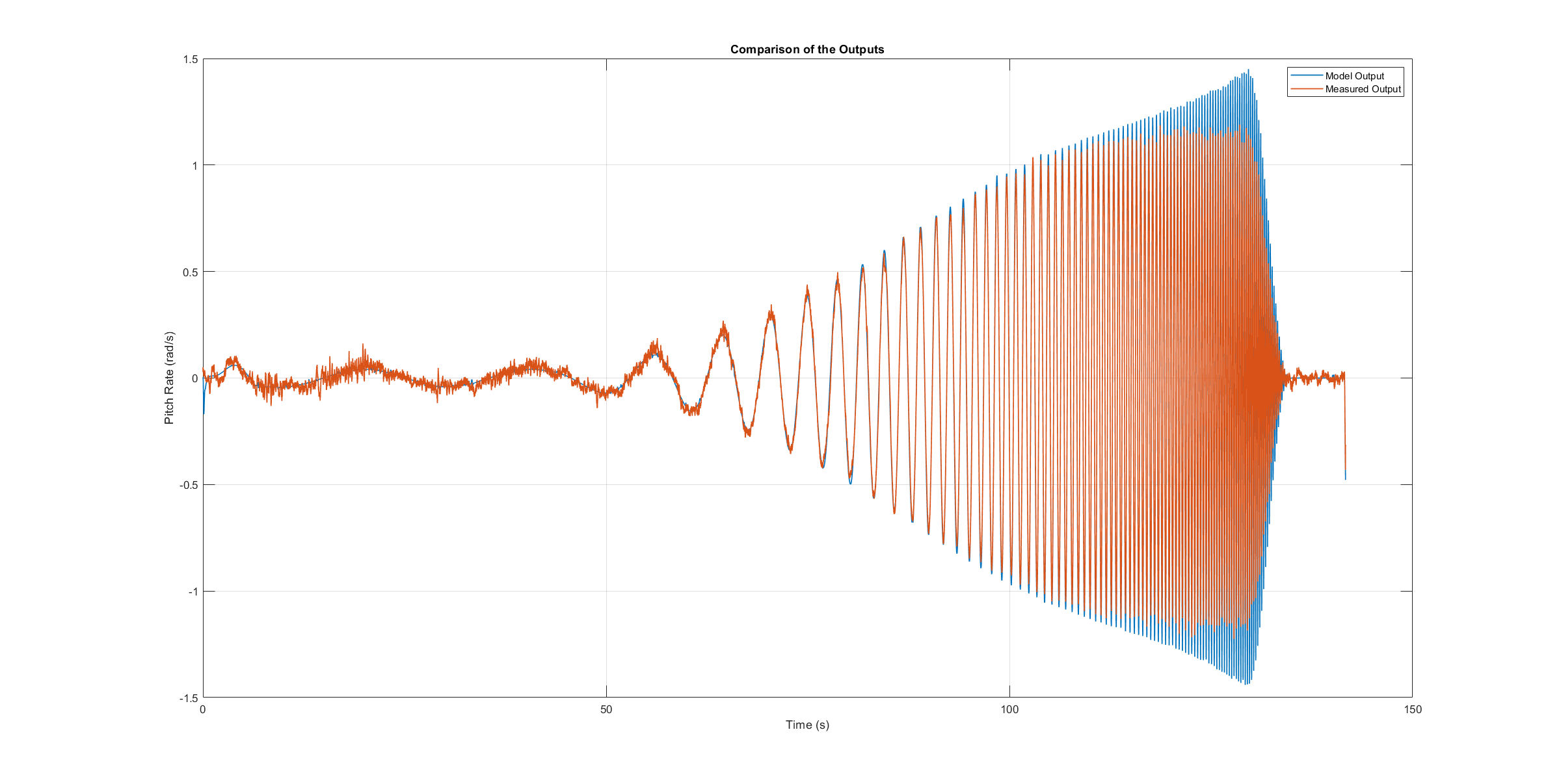
滚轴模型验证扫描
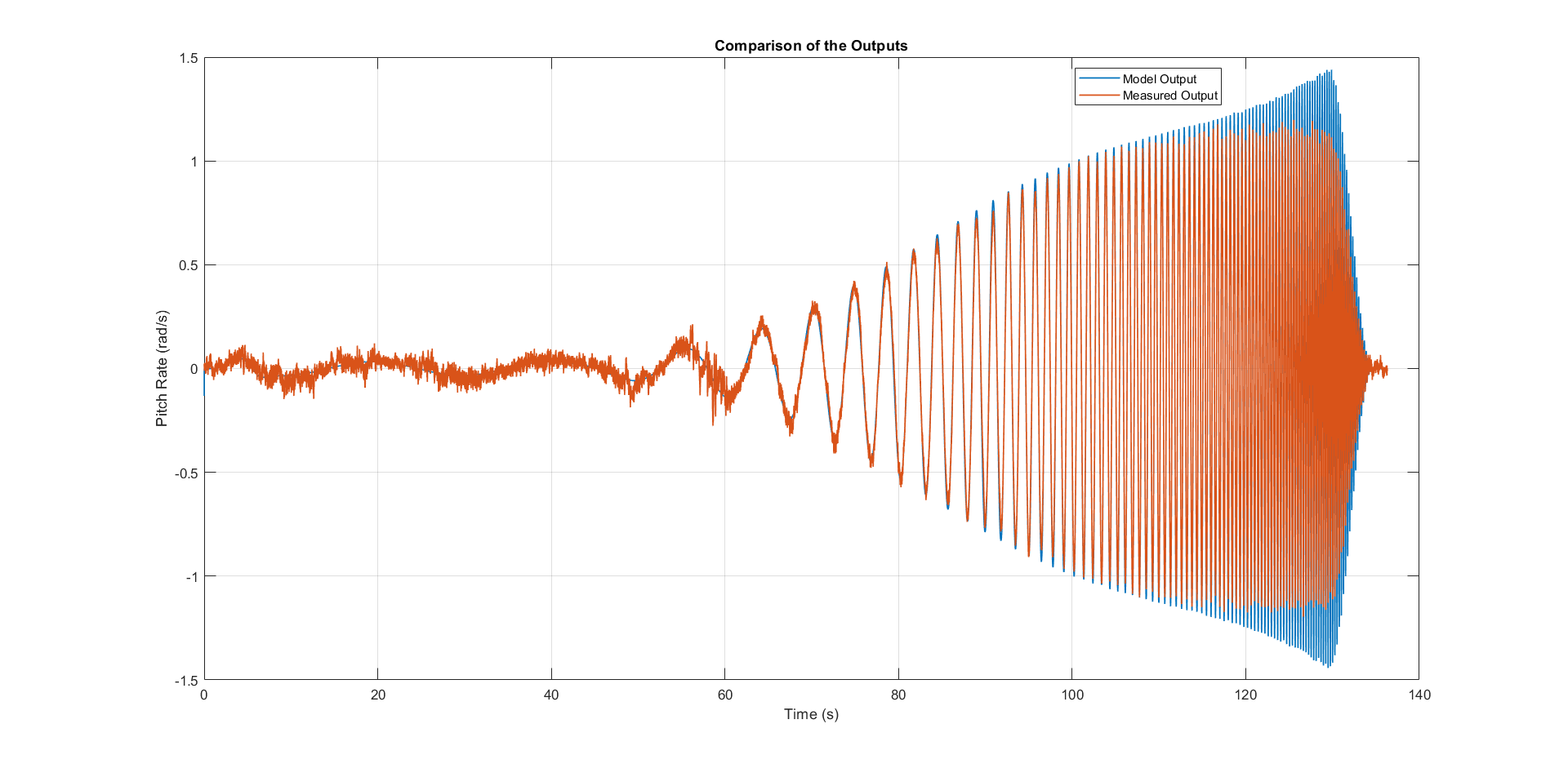
螺距轴模型验证扫描
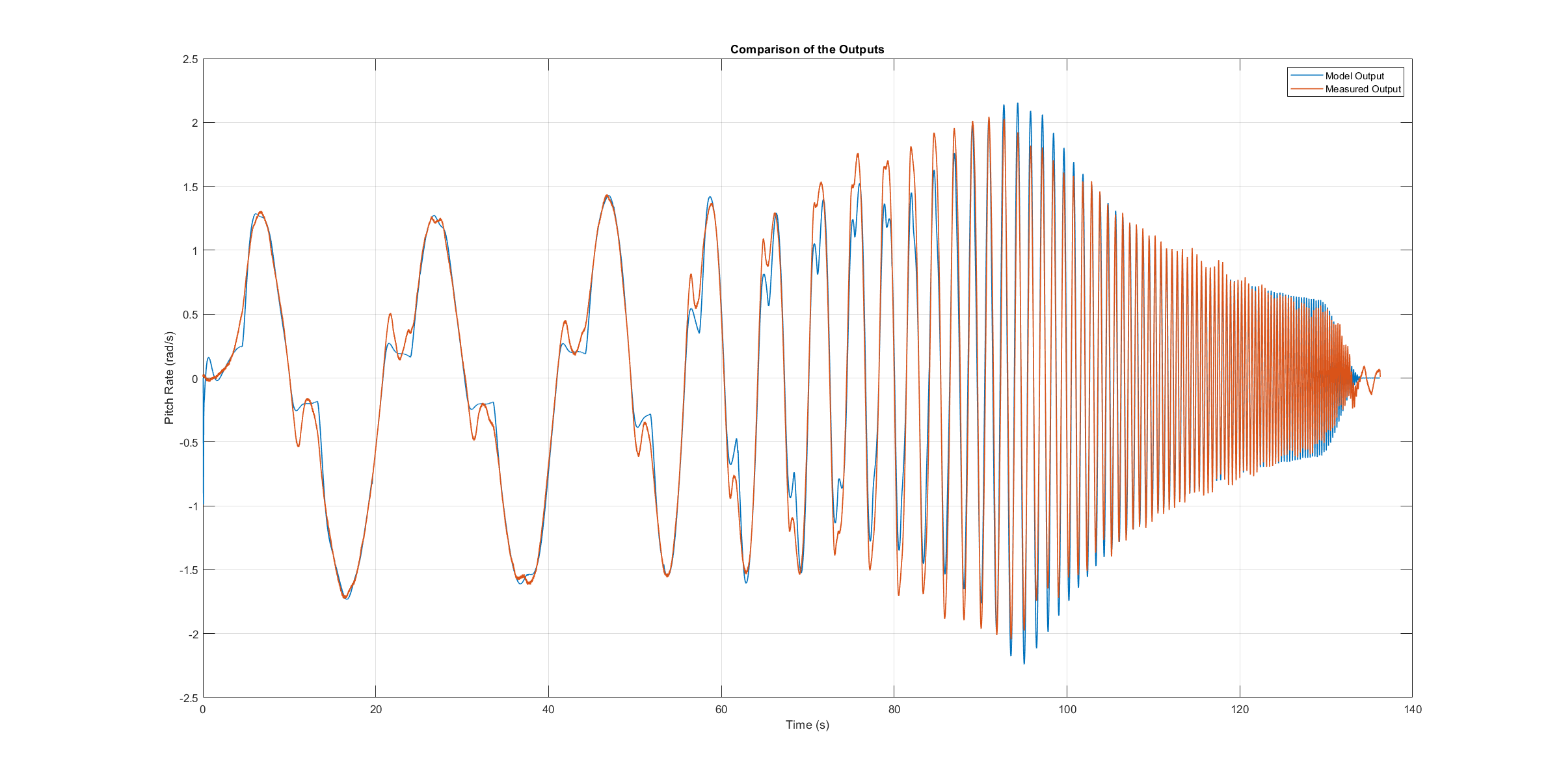
偏航轴模型验证扫描
由于频率扫描用于识别,因此必须用另一个测试信号对模型进行测试,以检查其稳健性。一个被广泛推荐的验证信号是所谓的双音频机动,它是一个双步进信号。 [8].为了进行时域验证,使用了类似的信号作为稳定控制器的输入。如下图所示,它由两个连续的双音频操纵组成。
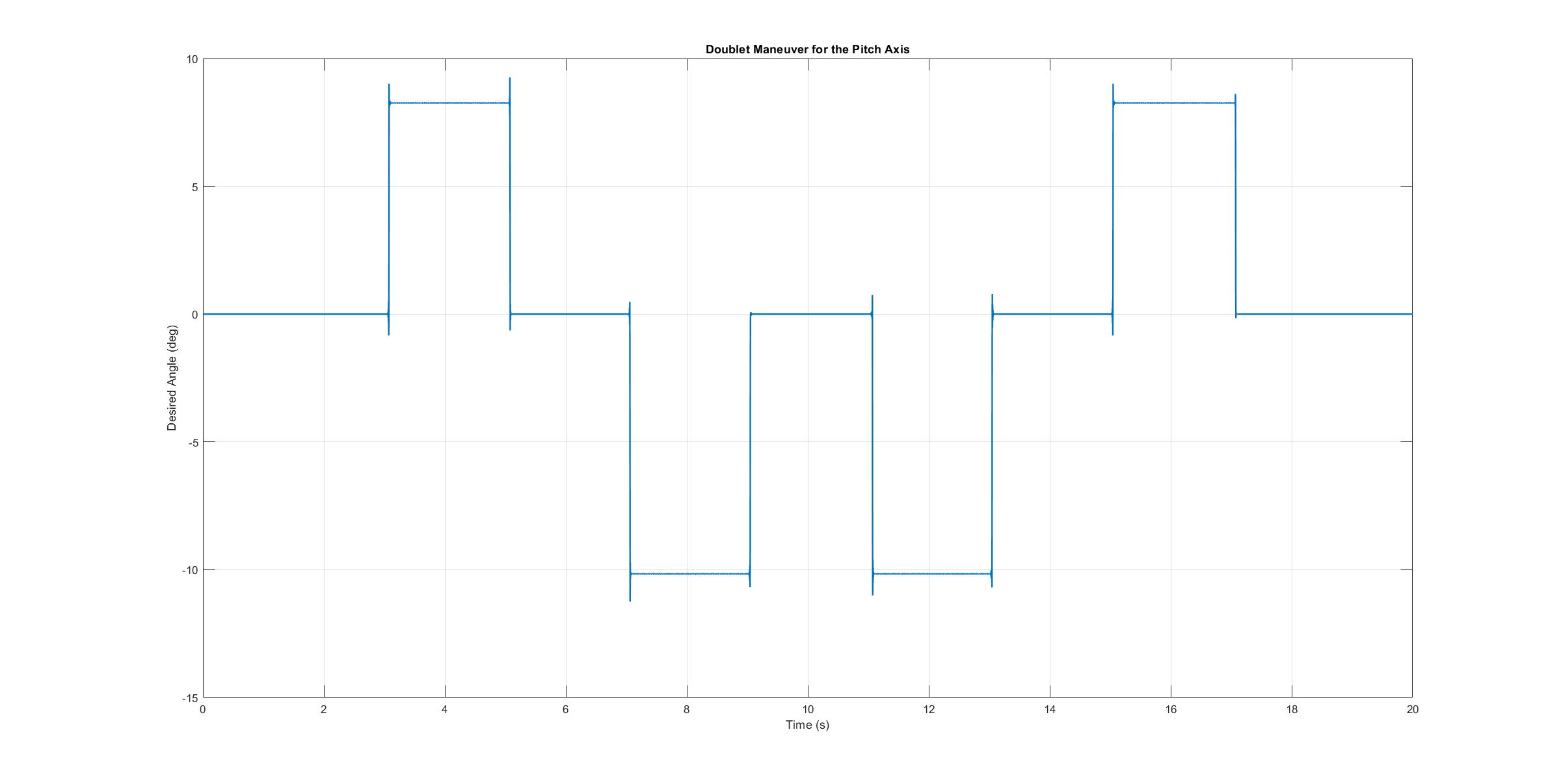
模型验证双重
接下来的三幅图包含了轴模型的角速率与验证飞行期间测量的角速率的对比。由于模型输出与测量角速率高度拟合,模型的保真度令人满意。
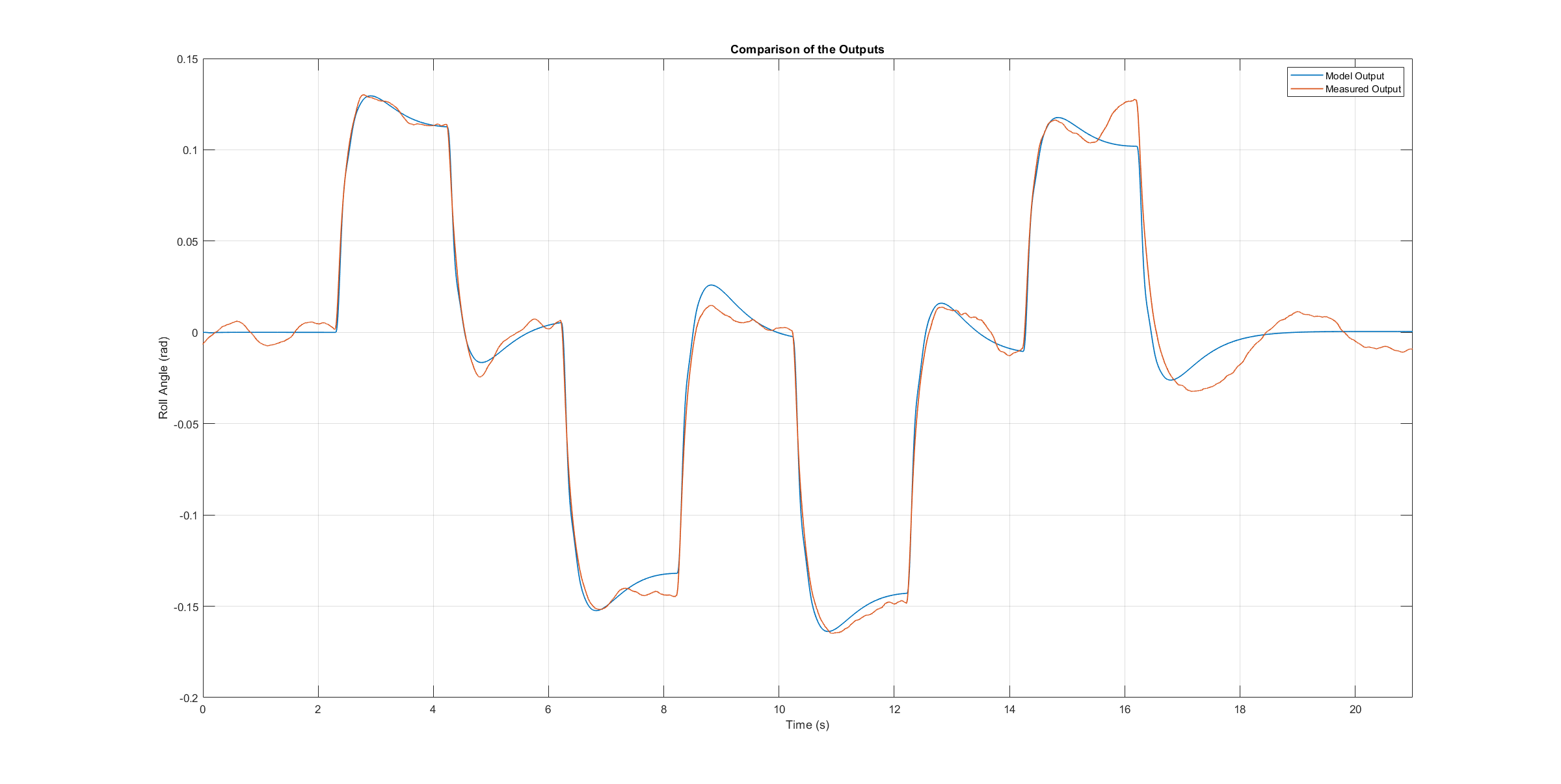
滚轴模型验证角速率
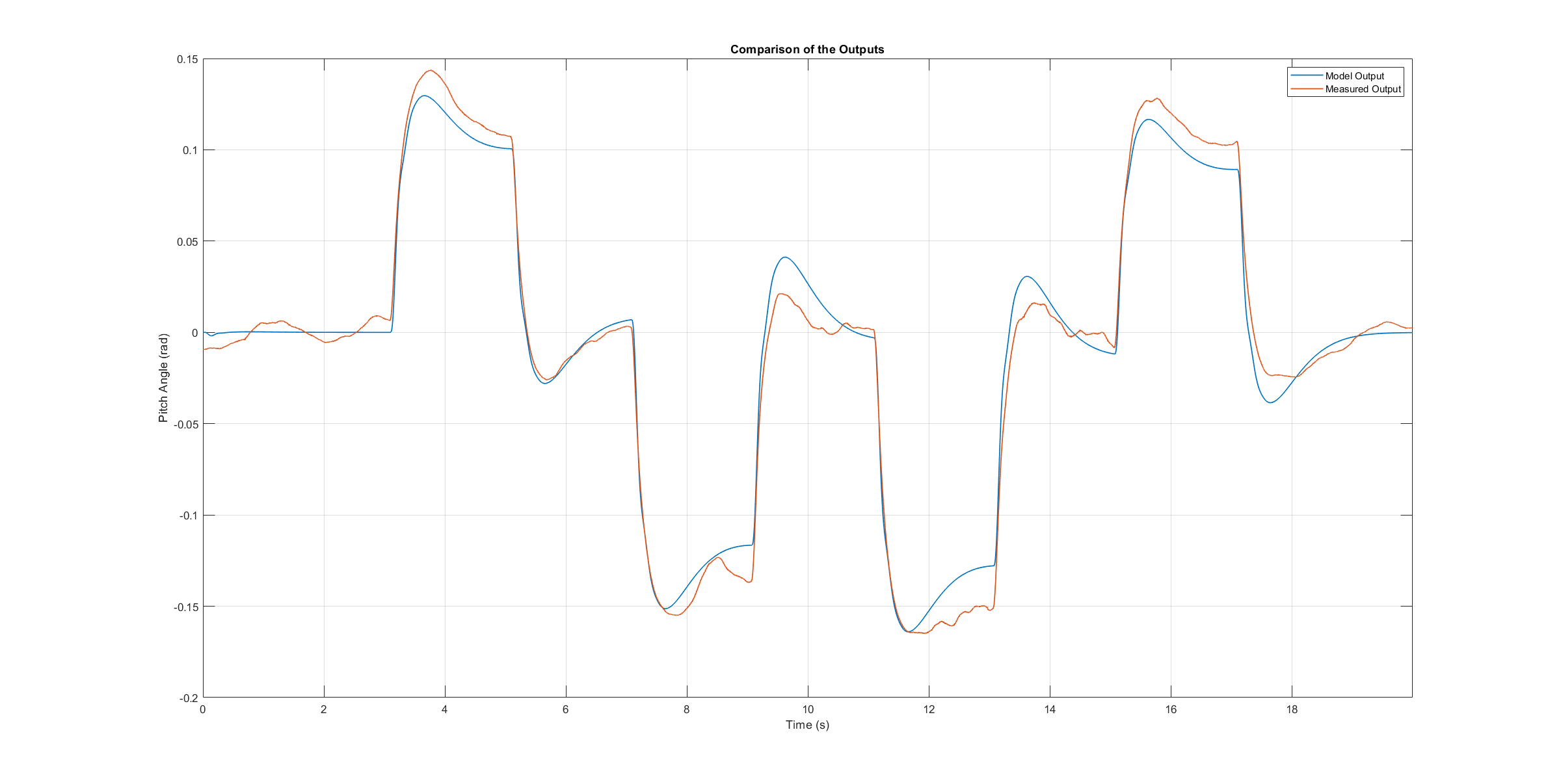
俯仰轴模型验证角速率
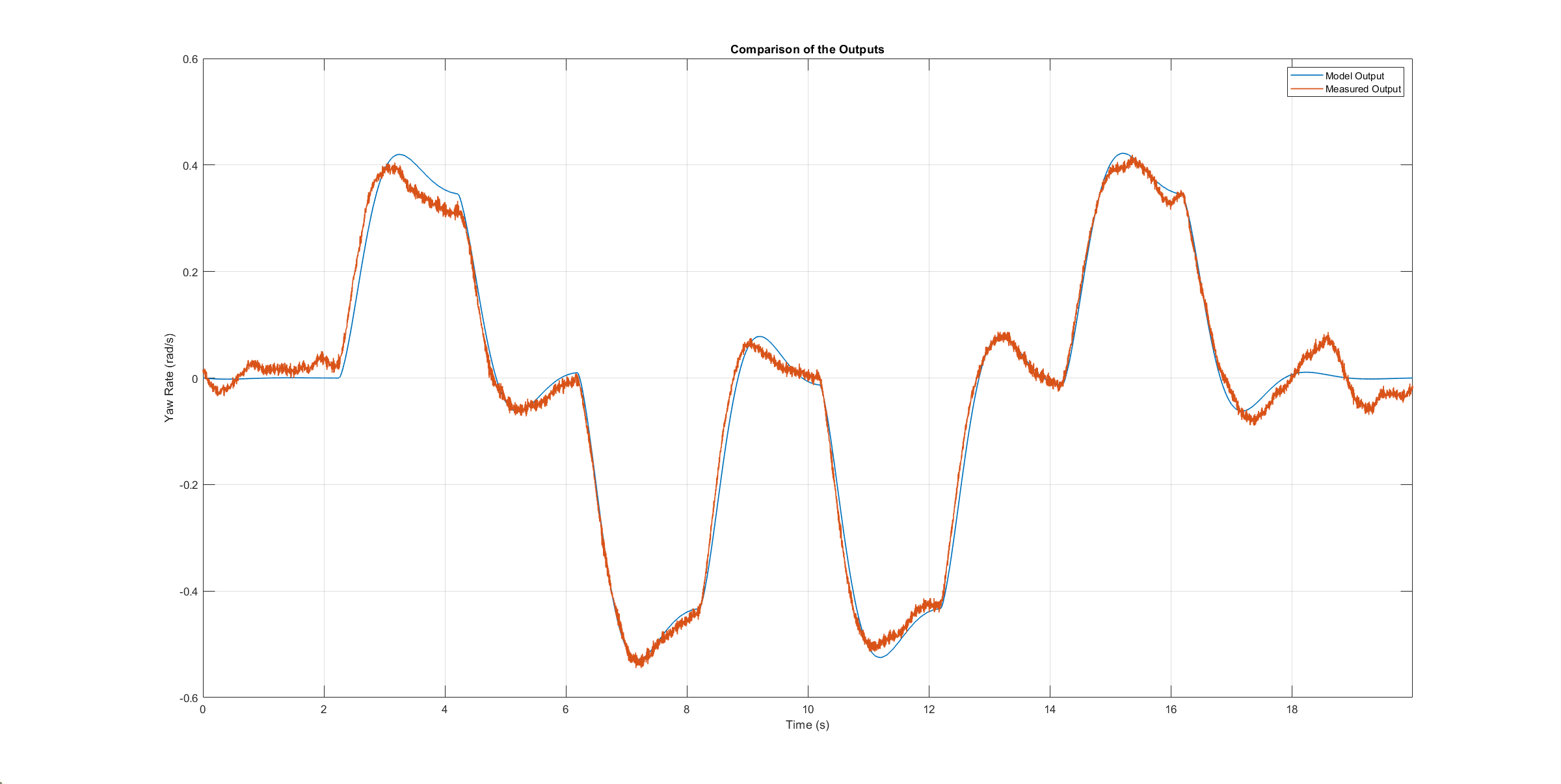
偏航轴模型验证角速率
获得载具模型后如何优化 PID¶
在上述章节中,我们推导并验证了多旋翼飞行器的分析数学模型。该模型可用于优化 ArduCopter 的 PID 参数。以下是优化过程的一个示例 这篇 ArduPilot 博文.
参考资料